Tips & Tricks: A faster search for patterns (loop, list, regexp)

In this article, we are going to take a look at one of the algorithms we wrote in Genome Toolkit series, Part 2, and attempt to optimize it. We will also discuss the approach a beginner in Python can take to learn how to write better, faster, and more Pythonic code. We will finish by measuring execution speed of all of our solutions, and discuss if it even is worth your time, to optimize your code.

A quick reminder of the problem we were solving with our kmer count algorithm:
Problem: Given a DNA/Genome string/sequence, and a k-mer, find how many times that k-mer appears in that sequence, including overlapping k-mers.

Our first and simplest solution, which is also easy to read and understand, was the for loop solution:

Generic, for loop solution:

def count_kmer_loop(sequence, kmer):
    kmer_count = 0
    for position in range(len(sequence) - (len(kmer) - 1)):
        if sequence[position:position + len(kmer)] == kmer:
            kmer_count += 1
    return kmer_count

In this solution, we just loop through the whole sequence, and check for k-mer match at each position. We use the position variable to shift the part we scan in the sequence.

Something like this:

if sequence[position:position + len(kmer)] == kmer
...
if AAT[TAA]AAC == AAA | do nothng
if AATT[AAA]AC == AAA | add 1 to count
...

for loop is easy to read and see every single step we are taking in our algorithm. It is also much easier to investigate with the Python Debugger. This should be the default approach when we are writing new algorithms. As long as it works as expected, and is fast enough for your needs, it is good enough. Python is fast enough to make this a viable solution for our algorithm.

List comprehension solution:

def count_kmer_listcomp(sequence, kmer):
    kmer_list = [sequence[pos:pos + len(kmer)]
                 for pos in range(len(sequence) - (len(kmer) - 1))]
    return kmer_list.count(kmer)

This example is almost the same as the loop approach, but a bit shorter. In this case, we just loop through our sequence again, and store k-mers in the list kmer_list. At the end, we just use one of the built-in list methods count to check how many times our k-mer appears in the list. We return the count. If we try visualizing it, it should look something like this:

seq = "AATTAAAAC"
kmer = "AAA"
kmer_list <= add [AAT]TAAAAC
kmer_list <= add A[ATT]AAAAC
kmer_list <= add AA[TTA]AAAC
...
count "AAA" in kmer_list

In the original loop solution we only used an integer variable that we incremented, based on the if statement when a k-mer match has been found. In the above List Comprehension solution, we used a list of k-mers we generated from the sequence, and after, we search for our k-mer in that list. This is not very efficient. It adds complexity and function/method calls. If the sequence is large, the list we generate will also be very large.

List comprehension is a strictly Python concept/syntax. This alone makes it not the best solution for a complex algorithm, in the case if we want to port (rewrite) it to a faster language in the future. Yes, it is short and still somewhat readable, but it is definitely less Python newbie-friendly.

The reason we looked at this example is that a lot of Python beginners seem to have an urge to write the most optimal, and shortest (fewer lines of code) code possible, in the early days of their Python journey. We end up with overcomplicated, hard to read, and hard to maintain code. That in most of the cases are also very slow. We will measure the execution speed at the very end of this article.

Now let’s take a look at our final solution.

RegExp solution:

from re import findall

def count_kmer_regexp(sequence, kmer):
    return len(findall(f'(?=({kmer}))', seq))

Regular expressions are another way of searching for k-mers in a string. This topic deserves a separate article, as RegExp is something you have to learn separately to be able to construct useful queries. Let’s break down the above example into 2 main parts:

1. We are using Python’s re module, and importing just the findall method from it.
   findall will allow us to search for all repeating patterns in a string, but, as we will see, it can’t search for overlapping patterns. We will need to use a regular expression to enable that.
2. (?=({kmer})) is a regular expression with positive Lookahead, that is wrapped in an F-String. This part allows the findall method to search for overlapping patterns. You can try using just the findall(kmer, seq) to see what results you will get.

Yes, regular expressions are not a simple concept, and it takes time to learn them. But the good thing about doing it, is that they are universal. You can use them in any programming languages, scripts, and spreadsheets.

There are a few tools that allow us to construct and test our regular expressions. I will link all of them after this part of the article. Let’s try looking at what such a constructor generates for us, with and without the positive Lookahead:

Without (no overlaps found), we find 3 patterns:

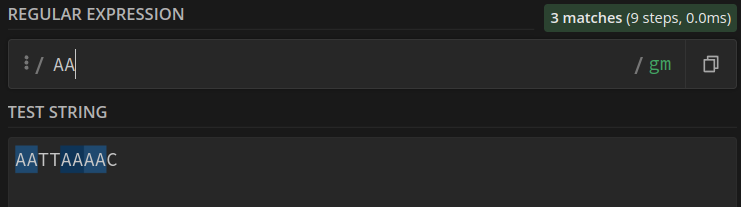
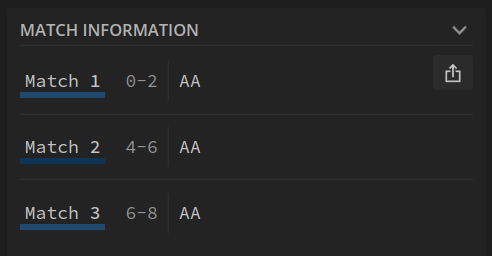
With (overlaps found) we find 4 patterns:

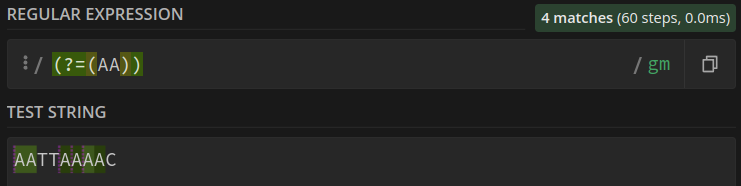
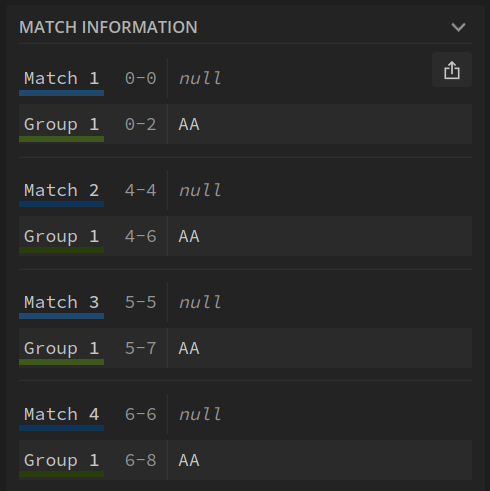
Now that we have used the tool to verify our regular expression, we can use it in our algorithm. It is as simple as passing a sequence and a k-mer, wrapped in a regular expression, to the findall method.

This is our last example. RegExp are definitely a complex topic, that has books dedicated to it. We looked at this example to illustrate the variety of solutions you can come up with, based on your experience.

Useful links about regular expressions in Python:

1. Regular Expressions generator/tester: https://regex101.com/
2. Regular Expressions for overlapping substring search: https://www.geeksforgeeks.org/python-program-to-find-indices-of-overlapping-substrings/
3. “Positive Lookahead” regular expression: https://www.rexegg.com/regex-lookarounds.html

Additional test: measuring execution speed

NOTE: You don’t have to implement this part and just review the provided results instead, unless you are interested in experimenting with timing your code.

There are many ways of measuring the execution speed of any part of your code. Let’s use the simplest, classic approach – timers. Python has multiple timing libraries built-in, and also third-party libraries. We will use the built-in one, called perf_counter. Let’s add it to the beginning of our file:

from time import perf_counter

Now we can just wrap our function calls into basic timing calls like so:

start_time = perf_counter()

# Call your code here...

elapsed_time = perf_counter()
execution_time = (elapsed_time - start_time):0.5f

If you print the execution_time, you should see the execution time in seconds. :0.5f part is making sure we round the number to the 5th decimal, to avoid long float numbers if our code runs very fast.

Before we add our timing code, let’s add the test data:

seq = "AATTAAAAC" * 100000
kmer = "AAA"

In the above data example, we take our sequence, and multiply it 100,000 times. This basically creates a new sequence that has the original sequence AATTAAAAC, repeating 100,000 times. This should stress our algorithm, and make it run for a bit longer, so we can measure time better.

Let’s now add a timing wrapper to all three of our solutions, to see which one takes less time to execute (I have added additional text to make the output more readable):

Loop solution:

start_time = perf_counter()

print("Loop k-mer counting: ", end='')
print(count_kmer_loop(seq, kmer))

elapsed_time = perf_counter()
print(f'Loop took: {(elapsed_time - start_time):0.5f}s\n')

List comprehension solution:

start_time = perf_counter()

print("List comprehension k-mer counting: ", end='')
print(count_kmer_listcomp(seq, kmer))

elapsed_time = perf_counter()
print(f'List comprehension took: {(elapsed_time - start_time):0.5f}s\n')

RegExp solution:

start_time = perf_counter()

print("RegExp k-mer counting: ", end='')
print(count_kmer_regexp(seq, kmer))

elapsed_time = perf_counter()
print(f'RegExp took: {(elapsed_time - start_time):0.5f}s\n')

If we now execute these three code snippets (you can add them after the functions, at the bottom of your .py file), we should see something like this:

Loop k-mer count: 200000
Loop took: 0.08382s

List comprehension k-mer count: 200000
List comprehension took: 0.10098s

RegExp k-mer count: 200000
RegExp took: 0.03228s

We can conclude, that RegExp is the fastest solution, finishing in about 0.03s.

Second fastest is actually the for loop solution, finishing in approximately 0.08s.

The slowest one is the List comprehension, finishing in 0.10s. These numbers will be different, depending on the speed of your computer, and also other applications you have running in the background.

Conclusion

What can we learn from this? A shorter solution, with fewer steps, does not mean it will run faster in every case. Generic for loop should be fast enough in most of the cases, when we are talking about simple algorithms. It is also very easy to read and understand. In a lot of cases, you can gain more performance by using some Python native packages and/or using the correct data structure for your case. In Genome Toolkit, Part 3 we will see an even better example of how changing how we store our k-mers will change the execution speed of the algorithm.

See you in the next article.

Video version: